БОЖЕСТВЕННАЯ МЕРА

В очерке Пять дней под кровом святителя Николая («Вера», № 668) упоминалось, как в наше время в Переславле-Залесском заново строился собор Свято-Никольского монастыря. Архитектор Вячеслав Ижиков использовал при этом древние меры, которыми в XI веке размерен был Свято-Успенский храм Киево-Печерской лавры. «Эти меры, как и точное указание, как строить, были даны в Византии строителям Самой Пречистой Девой. Царица Небесная вручила зодчим золотой пояс некого воеводы, пожертвованный Ей за чудесное спасение, – сообщает наш автор. – Длина этого пояса составила единицу расчётов при строительстве храма Киево-Печерской лавры. Вячеслав Николаевич смог узнать по архивным материалам длину меры. Но на этом зодчий не остановился – все пропорции собора исчислены ещё и с применением золотого сечения и расчислены на число 7 – число полноты Божией...» Этот факт заинтересовал некоторых наших читателей, и возник вопрос: «Что такое золотое сечение, является оно Божественной мерой или выдумкой язычников? Ведь пирамиды египетских фараонов тоже с помощью золотого сечения строились?»

Первым делом отметим, что не только золотое сечение, но и вообще все меры, основанные на закономерностях в природе, можно назвать божественными. Мир сотворён Богом, а посему всякое творение, даже искажённое грехом, носит на себе Его печать. Это относится и к материальным предметам, и к растительному и животному миру. Тем более это относится к человеку, о котором сказано, что он сотворён по образу и подобию Божию. И с самых древних времён тело человека было мерилом длины, пока на смену этому не пришли меры искусственные.

Сейчас длину мы измеряем с помощью метров, где один метр, если считать по-старому, равен 39,37 дюйма. А что такое дюйм? С нидерландского языка это переводится как «большой палец» и соответствует ширине большого пальца среднего мужчины. Прежде в дюймах («пальцами») измеряли всюду в Европе. А потом случилась революция. Сейчас её принято называть «научно-технической», но, конечно, она коснулась не только науки и техники – это был глубинный переворот в мировоззрении людей, сопровождавшийся атеизмом и социальными бунтами. Неслучайно идея ввести международную метрическую систему родилась не где-нибудь, а во Франции, откуда по всему континенту распространялись в ту пору революционные настроения. Сразу после Великой французской революции идея «метра» быстрыми темпами стала материализовываться. В 1795 году Конвент Французской Республики поручил комиссарам, в число которых входили знаменитые учёные Кулон, Лагранж и Лаплас, выполнить работы по экспериментальному определению единиц длины и массы. К тому времени уже было начато измерение дуги парижского меридиана от Дюнкерка до Барселоны, работа продолжалась шесть лет. В итоге учёные постановили, что метр равен одной десяти миллионной части расстояния от Северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа. В 1799 году французы изготовили эталон метра – брусок из сплава платины и иридия с двумя насечками. Был сделан и эталон килограмма, привязанный к метру (1 кг – это масса кубического дециметра воды).

При Наполеоне Бонапарте метрическая система быстро распространилась по Европе. Только в Британской и Российской империях, которые не были завоёваны Наполеоном, остались нетронутыми традиционные меры длины. В англоязычных странах и поныне расстояние измеряют с помощью «ширины большого пальца» (английский дюйм равняется 2,54 сантиметра). Противники метра нашлись и в других странах, причём учёные сами не знали, как объяснить неприятие этой системы. Берлинский астроном Боде упорно отказывался публиковать в своём научном журнале материалы о метрической системе, ссылаясь на то, что он «имеет честь и счастье жить в стране с монархическим правительством». Известный английский философ Г. Спенсер написал даже брошюру «Против метрической системы». Люди самого что ни на есть рационалистического склада ума не хотели признавать очевидный факт: метрическая десятеричная система удобней для научных измерений и последующих вычислений. Сами же они постоянно сталкивались с путаницей разномерных футов и дюймов. Фут (с английского языка переводится как «ступня») в ту пору в Европе обозначал 282 (!) различные единицы длины. Схожая ситуация была и с дюймом, который всюду имел разную длину. Скажем, придуманная датчанином Гансом Христианом Андерсеном девочка Дюймовочка в одной только Германии имела пять разных ростов: в Баварии – 2,43 см, в Бадене – 3 см, в Пруссии – 2,61 см и т. д. Откуда же взялось такое упорное неприятие новой, более удобной системы измерений? Помимо привычки, наверное, было инстинктивное ощущение, что человечество, отбросив «человеческую меру», утратит живую, реальную связь с тем, что этой мерой измерялось.

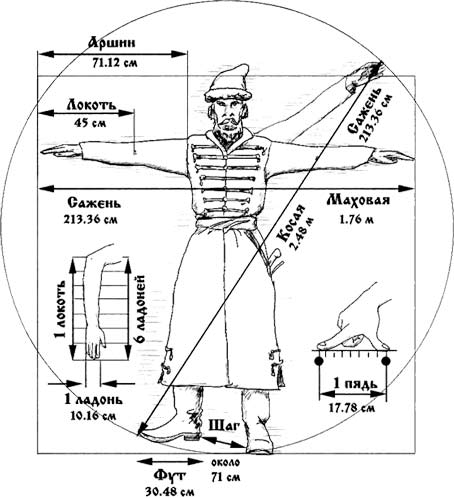
Надо сказать, Российская империя была среди 17 государств, которые ещё в 1875 году в Париже подписали международную конвенцию о необходимости введения единой метрической системы. Но на Руси «французские выдумки» так и не приняли. Только в 1899 году, перед наступлением нового ХХ века, Государь подписал соответствующий закон, проект которого разрабатывался Д. И. Менделеевым. Но даже по этому закону метрическая система была лишь допущена к применению «в необязательном порядке». Русские люди по-прежнему мерили длину в саженях, локтях и аршинах (см. на рисунке) – вплоть до советского декрета от 14 сентября 1918 года.

Платиновоиридиевый брусок, изготовленный французами в 1799 году, до сих пор хранится в Международном бюро мер и весов в предместье Парижа. Но сейчас это уже музейный экспонат. В 1960 году учёные решили отказаться от применения изготовленного людьми предмета в качестве эталона метра и взяли более точный эталон – число 1 650 763,73, умноженное на длину волны «оранжевой линии» спектра, излучаемого изотопом криптона-86 в вакууме. А спустя два десятилетия решили отказаться и от этого. С 1983 года метром принято считать длину пути, который проходит свет в вакууме за 1/299792458 долю секунды.

Можно ли метр назвать божественной мерой? Как выше мы увидели, для его определения использовалось то, что и вправду относится к творению Божьему: сначала это была размерность планеты (часть земного меридиана), затем спектр и скорость света. Но это всего лишь «использовалось». Сама же мера была взята не из природы, а из абстрактного десятичного счёта. Ведь метр «появился», когда часть земного меридиана поделили на число 10000000. Существует ли такое десятичное число в реальном Божьем мироздании? На обеих руках человека – 10 пальцев, что когда-то подвигло людей (в частности, в Древнем Египте) за основу счёта взять десяток. Но это всё-таки случайная, произвольная цифра, она нигде в природе не повторяется. Физики находят реальные закономерности в мироздании, связанные с двоичностью, троичностью или с семиричностью (самая известная – семь цветов, которые выделил из непрерывного спектра радуги Исаак Ньютон), но ничего десятичного нигде не проглядывает. Получается, что 10 – совершенно абстрактное, «несуществующее» число. Оно ни с чем не соотносится, и к чему бы реальному мы его ни прилагали, всегда в итоге получим «дробность», множество цифр после запятой. Например, золотое сечение, которое в средние века именовали божественной пропорцией, в десятичной системе выражается цифрой 1,61803398875... Впрочем, даже отражённая в искусственной системе счисления, эта пропорция показывает удивительные свойства, разгадку которых ищут до сих пор.

Принято считать, что понятие «золотое сечение» ввёл в научный обиход грек Пифагор (VI в. до н.э.). Также предполагают, что своё знание он позаимствовал у египтян, те – у вавилонян, а те, в свою очередь, у древних шумеров, хранивших от времён Адама и Евы множество преданий, которые хоть и в искажённом виде, но частично совпадают с библейскими. Действительно, если внимательней присмотреться к пирамидам Хеопса, к барельефам, украшениям из гробницы Тутанхамона в Египте, а также к предметам вавилонской и шумерской культуры, то всюду увидим золотое сечение. Этот факт отмечали и древний мудрец Платон (в сочинении «Тимей», V в. до н.э.), и современный архитектор Ле Kорбюзье, изучавший пропорции древних строений.

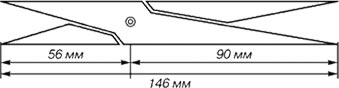
Особенный интерес к золотому сечению проявился в Западной Европе в эпоху Ренессанса, когда художники и архитекторы идеал красоты увидели в «золотых» пропорциях античных памятников. Чтобы систематизировать это древнее знание, Леонардо да Винчи начал писать книгу по геометрии, но вскоре бросил это начинание, поскольку его опередил монах-францисканец Лука Пачоли. В 1509 году в Венеции была напечатана его книга «Божественная пропорция» с блестяще выполненными иллюстрациями (предположительно, их нарисовал всё тот же Леонардо да Винчи). Книга была восторженным гимном золотой пропорции. На рисунке ниже хорошо видно «золотое» соотношение частей в храме Парфенона (г. Афины) и, для примера, античного циркуля, сделанного с учётом золотого сечения.

Античный циркуль

Одна его часть (90 мм) больше другой (56 мм) – ровно настолько, чтобы получилось гармоничное, «золотое», соотношение между ними. Насколько такое соотношение действительно гармонично, можно убедиться, созерцая фасад античного здания (на рисунке ниже).

Как видим, здание имеет несколько пропорций. Между антаблементом (фризом с карнизом) и крышей. Между антаблементом с крышей и колоннами с цоколем-стилобатом. Между колоннами. Здесь все пропорции между большими и малыми частями являются «золотыми». Соотношение их можно выразить одной и той же величиной – дробной цифрой 1,6. Проще говоря, если высоту крыши мы поделим на высоту антаблемента, то именно это «золотое число» – 1,6 – и получим.

Примечательно, что православные за много веков до Луки Пачоли восхищались гармонией золотого сечения. По некоторым сведениям, храм Парфенона (тот, что показан на рисунке) при святителе Павле, Патриархе Константинопольском († 784), был переоборудован в храм Святой Софии. По другим сведениям, он стал православным ещё раньше, за двести лет до этого. Точно известно, что во времена Византии парфенонский храм служил православным кафедральным собором Пресвятой Богородицы и был четвёртым по значимости паломническим центром Восточной Римской империи – после Константинополя, Эфеса и Салоник. Например, в 1018 году император Василий II прибыл в Афины после блестящей победы над болгарами с единственной целью – поклониться православным святыням, находившимся в стенах храма Парфенона. Вообще же в Византии, в отличие от Западной Европы, технические архитектурные приёмы античности не были забыты и широко применялись. Так, перед началом строительства собора Святой Софии в Константинополе один из главных зодчих, Исидор из Милета, обобщил труды Архимеда и составил комментарий к сочинению Герона Александрийского о конструкции сводов. Приёмы античного зодчества дополнялись и творчески перерабатывались, в результате чего со временем и появился византийский архитектурный стиль. От античности были взяты два типа построек – центрические и базиликальные. И конечно, было унаследовано золотое сечение.

Но вернёмся в Западную Европу, где учёный-католик Лука Пачоли восхищался открытым им золотым сечением. С простодушием и восторженностью францисканца он писал в своей книге «Божественная пропорция» о некоей её «божественной сути» – как выражении триединства Бога. При этом он так рассматривал части пропорции: малый отрезок – это олицетворение Бога Сына, большой – Бога Отца, а весь отрезок – Бога Духа Святого. Это триединство, по мнению монаха, было разлито во всей природе, в том числе отразилось и в теле человека, который создан по образу и подобию Божьему. Вскоре с Пачоли встретился приехавший в Италию немецкий художник Альбрехт Дюрер и стал разрабатывать свою знаменитую теорию пропорций человеческого тела, где важное место было отведено золотому сечению. В том же XVI веке великий астроном Иоганн Kеплер назвал золотое сечение «одним из сокровищ геометрии». Он первый обратил внимание на значение золотой пропорции для ботаники (рост растений и их строение). Но на этом изучение великой загадки в ту пору и закончилось.

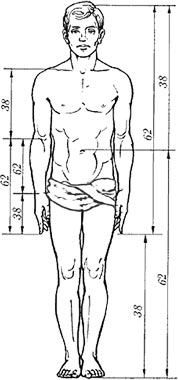
Вновь о золотом сечении заговорили только в середине XIX века. В 1855 году немецкий профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он объявил пропорцию золотого сечения универсальной для всех явлений природы и искусства. Сам он проделал огромную работу – измерил около двух тысяч человеческих тел – и пришёл к следующему выводу. Если рост человека поделить на две части, проведя черту на уровне пупа (той точки, где присоединялась пуповина, дававшая жизнь в утробе матери), то пропорция этих частей в среднем будет «золотой». 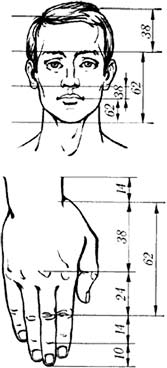Причём пропорции мужского тела колеблются в пределах среднего отношения 13:8 = 1,625 (три цифры после запятой) и несколько ближе подходят к золотому сечению 1,61803398875..., чем пропорции женского тела, среднее значение которых выражается в соотношении 8:5 = 1,6 (одна цифра после запятой). У новорождённого пропорция составляет отношение 1:1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длин плеча, предплечья и кисти, кисти и пальцев и т. д.

Позже было открыто, что и внутренние органы человека также имеют золотое сечение. Наши современники, физик Б. Уэст и доктор А. Гольдбергер, подметили, что бронхи, состоящие из двух основных дыхательных путей, короткого и длинного, имеют интересную асимметрию: соотношение их длин составляет золотое сечение и равно 1:1,618 – то есть золотую пропорцию с точностью до трёх знаков после запятой. Такая «золотая» асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях лёгких человека. Что уж говорить, даже в ДНК учёные обнаружили «божественное число» – в соотношении длины и ширины двух спиралей в молекуле.

Что же касается теории Цейзинга, то он её проверял не только на «живой натуре», но и на греческих скульптурах, которые считаются идеалом красоты, в том числе на статуе Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, музыкальные тона, стихотворные размеры. Как ни удивительно, но в простом птичьем яйце, какие мы красим на Пасху, тоже обнаружилась явная «божественная пропорция»:

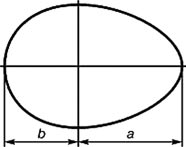
Цейзинг выпустил книгу «Золотое деление как основной морфологический закон в природе и искусстве», которая под псевдонимом была издана и на русском языке в 1876 году. А в начале 1900-х американский математик Марк Барр использовал греческую букву φ для обозначения золотой пропорции – и с той поры «божественное число» 1,61803398875... стало использоваться в математике наряду с числом π (3,14159265358...) и другими математическими константами.

Что интересно, число φ (произносится как „фи“) Барр назвал по имени Фибоначчи, монаха из Пизы, жившего в XII-XIII веках. В 1202-м Леонардо Фибоначчи выпустил математический труд «Книга об абаке» (счётной доске), в котором были собраны все известные на то время арифметические задачи. Одна из задач гласила: «Сколько пар кроликов в один год от одной пары родится?» Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

0 1 1 2 3 5 8 13 21 34 55 89 144 и т. д.

Сейчас эта последовательность известна как «ряд Фибоначчи». Особенность в том, что каждый член этого ряда, начиная с третьего, равен сумме двух предыдущих: 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т. д. А если соседние цифры не складывать, а делить, то мы получим... приближение всё к тому «золотому» числу 1,61803398875...! Например, 8:5 = 1,6; 13:8 = 1,625; 21:13 = 1,61538461538... И так далее. Заглянем в ряд Фибоначчи подальше от его начала: 317811:196418 = 1,61803398873...; 832040:514229 = 1,61803398874... Как видим, с «золотым» числом φ совпадает уже до десятого знака после запятой. Но это всего лишь приближение к искомому числу, и оно может длиться столь бесконечно, сколь бесконечна сама дробность иррационального числа.

Как пишет Виктор Лаврус, руководитель Киевского центра внедрения информационных технологий, ряд Фибоначчи мог бы остаться математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходят к этому ряду как арифметическому выражению закона золотого деления. В наше время учёные продолжают активно развивать теорию чисел Фибоначчи и золотого сечения. Так, Ю. Матиясевич с использованием чисел Фибоначчи решил десятую проблему Гильберта (это одна из 23 «неразрешимых» задач, сформулированных в 1900 году на II Международном конгрессе математиков). С их помощью появились изящные методы решения различных кибернетических задач (теории поиска, игр, программирования), а в США возникла даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Факты, подтверждающие существование золотых сечений в природе, приводит и белорусский учёный Э. Сороко в книге «Структурная гармония систем». Оказывается, что хорошо изученные двойные сплавы обладают особыми, ярко выраженными функциональными свойствами (устойчивостью в термическом отношении, твёрдостью, износостойкостью, устойчивостью к окислению и т. п.) только в том случае, если удельные веса исходных компонентов связаны друг с другом одной из золотых пропорций. Это позволило учёному выдвинуть гипотезу, что золотые сечения есть числовые инварианты самоорганизующихся систем. Если эта гипотеза подтвердится экспериментально, то она будет иметь фундаментальное значение для развития синергетики – новой области науки, изучающей процессы в самоорганизующихся системах.

Изучение математиками золотой пропорции позволяет им говорить о возможности создания новой системы счисления. Как известно, в десятичной, пятеричной, двоичной и других классических системах счисления в качестве первоосновы были выбраны натуральные числа 10, 5, 2, из которых уже по определённым правилам конструировались все другие натуральные, а также рациональные и иррациональные числа. Если же за основу счисления взять число φ (то самое «божественное число» золотой пропорции), то в такой системе счисления любое натуральное число всегда будет представимо в виде конечной, а не бесконечной, как думали ранее, суммы степеней любой из золотых S-пропорций. Впрочем, человеку, далёкому от математики, в этом трудно разобраться. Остаётся только поверить Виктору Лаврусу, который утверждает, что такая «иррациональная» арифметика, «обладая удивительной математической простотой и изяществом, вберёт в себя лучшие качества классической двоичной и "Фибоначчиевой" арифметик».

Как бы там ни было, золотое сечение – одна из самых заметных доминант мироздания. В отличие от других фундаментальных физических констант – скорости света в вакууме, гравитационной постоянной и др., – золотое сечение проявляет себя эстетически, мы видим в нём красоту Божьего мира. Оно заключено в спирали морской раковины и в спиралевидной форме галактик (в соотношение «шагов» развёртывания спирали), в строении ящерицы (в соотношении длин туловища и хвоста), в расположении листьев на ветке... Как, например, растёт ничем не примечательное растение цикорий? Вот от стебля отпочковывается отросток и даёт первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок меньшего размера и т. д. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвёртый – 24 и т. д. – то есть следуя ряду Фибоначчи по закону золотого сечения. Длина лепестков также подчинена золотой пропорции:

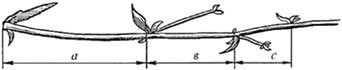
Из особой асимметричности растительного мира ботаники выводят «формулу красоты», которая, возможно, перешла к нам из Эдемского сада (подробнее см. в статье Ремесло Адама в № 535 «Веры»). И удивительно видеть в нашей падшей вселенной отблески этой красоты. Разве можно назвать совпадением тот факт, что строение живых организмов и неживых объектов, не имеющих никакой связи и подобия между собой, устроены по одному и тому же закону красоты? По нему сотворены галактики, растения, микроорганизмы, кристаллы, живые существа, молекулы ДНК, законы физики... Нам лишь остаётся созерцать эту красоту и повторять её в своём творчестве, в том числе в пропорциях храмов, славящих Господа.

В завершение следует сказать, что с древних времён в храмостроительстве использовалась не только золотая, или, как её называли в средние века, божественная пропорция, данная нам опосредованно через Божье творение. В Библии описывается, как Господь напрямую дал Моисею и Соломону подробные указания о размерах ветхозаветного храма и его пропорциях. На Руси же при строительстве некоторых церквей использовалась мера длины пояса Божией Матери.

Как известно, повсеместное храмостроительство у нас началось с Киева, сердцем которого была Киево-Печерская лавра, а главным её храмом был собор Успения Божией Матери. Заложили его при князе Святославе, который пожертвовал на строительство сто гривен золота. Киево-Печерский патерик сообщает, что большой вклад в строительство сделал и варяжский воевода Шимон (в крещении Симон). История его следующая. В Скандинавии был известен Якун Слепой, которого некоторые историки считают сыном шведского короля Олафа и, следовательно, шурином Великого князя Ярослава Владимировича Мудрого. Якун (Иаков) не раз помогал киевскому князю в борьбе с врагами. У Якуна был брат – князь Африкан, имевший двоих сыновей – Фриянда и Шимона. После смерти Африкана Якун изгнал племянников.

Перед тем как отправиться в изгнание, Шимон встал на молитву в домовой церкви у родового образа Распятия. На Распятии висели две святыни – пояс и венец. Происхождение их неизвестно. Предполагают, что варяги захватили их при набеге на Константинополь. Но, скорее всего, это были точные копии венца Христова и пояса Богоматери, изготовление которых было распространено в Европе. Например, такая реликвия с IX века хранилась в бенедектинском монастыре Нотр-дам де Лош. Вообще для Запада IX–XII веков было характерно почитание «метрологических» святынь: так в вюртенбергском аббатстве Бебенгаузен почитались меры длины Тела Христова и Гробницы Богоматери. Во время молитвы Шимон услышал глас, который повелел ему идти на Русь, взяв с собой пояс и венец от Распятия. Шимон снарядил корабль и отплыл в неведомую землю. В море судно настигла буря, и, теряя надежду на спасение, варяг Шимон взмолился к Богу. Он увидел в небесах неземной красоты церковь и вновь услышал голос свыше, предсказавший ему, что сейчас он останется невредим, а в будущем сподобится участвовать в строительстве церкви, где и будет погребён. В откровении ему были сообщены размеры храма, который надлежало построить, и указана мера – взятый им пояс Богородицы. Затем Божий Промысл привёл варяга к преподобному Антонию Печерскому. Перед битвой с половцами старец сказал Шимону, что русичи потерпят поражение, но сам он останется в живых. Также преподобный подтвердил предсказания о том, что построена будет в Печерской обители церковь, в которой по кончине упокоится Шимон. Возвратившись из неудачного похода, Шимон отдал преподобному венец и пояс и рассказал всё, что стало известно ему из откровений о строительстве «небеси подобной» церкви. И всё было исполнено.

Позже, по свидетельству патерика, этот пояс стал мерой для постройки целого ряда Богородичных храмов на Руси, в том числе Успенской церкви в Ростове и Успенской церкви в Суздале. Поначалу пояс, как и заповедано было, хранился в соборе Лавры, а затем, по некоторым сведениям, Владимир Мономах увёз его в Суздаль.

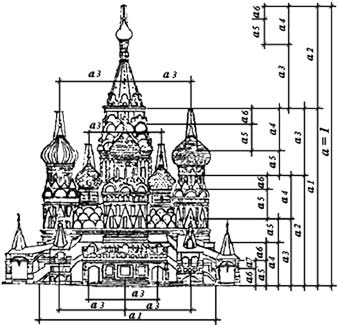
Это только одна история... Когда смотришь на древнерусские храмы, возведённые с молитвой, почему-то блекнет образ греческого Парфенона, построенного с математической точностью по законам золотого сечения. Эти русские церкви кажутся живыми. Да, в них тоже есть «божественное число» 1,618 – ведь зодчие использовали русские меры, аршины да сажени, в которых заключены пропорции тела человека с их золотым сечением. Но, кроме этого, чувствуется ещё что-то неуловимое. Всё-таки есть вещи, которые невозможно измерить и выразить в цифрах! Может, в них и заключена истинная Божественная мера?